Após quase 60 anos, “problema do sofá” da matemática pode ter sido resolvido

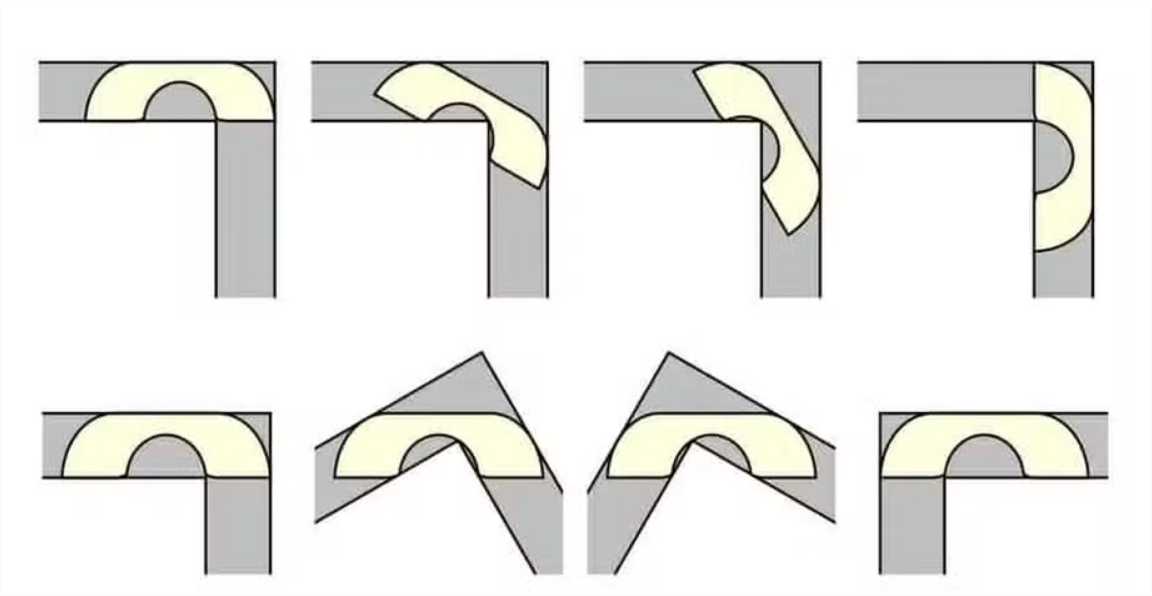
Basicamente, o problema discute como mover um sofá curvo dentro de um corredor estreito, que apresente um canto de 90°. Muitas pessoas já viveram na pele essa situação ao se mudarem para uma casa nova, porém, a questão, se vista sob um olhar analítico, é mais complicada do que parece.

Como lembra o site IFLScience, a grande pergunta é: qual a região de maior área que pode ser movida em torno de um canto reto em um corredor?

Histórico de tentativas de resolução

O problema foi formulado pela primeira vez em 1966 pelo matemático Leo Moser. Ele já circulava há anos em encontros científicos, mesmo sem nunca ter sido resolvido. Inicialmente, a questão não considerava um sofá sendo transportado, mas, sim, um piano.

A terminologia do móvel só passou a ganhar notoriedade com a definição de seu formato por um artigo de John Hammersley, publicado em 1968. Na ocasião, o texto propôs um sofá em formato de meia rosquinha – um clássico dos anos 1950 e 1980. E, assim, demonstrou com cálculos relativamente simples que a resposta sobre a maior área possível seria de (π/2) + (2/π), aproximadamente 2,2074.

Contudo, a euforia de uma resposta durou pouco. No mesmo artigo, Hammersley conseguiu chegar a outro resultado que indicava o limite superior da área como o resultado de 2√2, ou cerca de 2,8284. Comparados, os valores apresentavam uma grande janela de diferença, o que fez com que a comunidade matemática voltasse a analisar a questão.

Somente 25 anos depois que outro matemático entrou em cena: Rutgers Joseph. Ele pensou em um sofá construído a partir de 18 seções de curvas conectadas analiticamente suaves – o “sofá Gerver”, como ficou conhecido. O resultado foi de um limite de 2,2195.

Mais um quarto de século passou até que o intervalo de soluções possíveis fosse reduzido ainda mais. Em 2018, a dupla Yoav Kallus e Dan Romik usou uma prova assistida por computador para atingir o limite de 2,37. Mesmo sendo uma grande melhoria em relação aos limites originais de Hammersley, ainda não era uma solução exata para o problema.

Uma solução por fim?

Teria sido mais ou menos na mesma época em que Kallus e Romik estavam trabalhando em sua solução que Jineon Baek começou a pensar sobre o problema do sofá. Agora, sete anos depois, ele avalia que o decifrou em uma prova que abrange mais de 100 páginas de análises, publicadas ainda sem revisão no servidor de pré-impressão ArXiv.

“Dediquei muito tempo a isso, sem nenhuma publicação até agora”, afirmou o pesquisador à revista New Scientist. “O fato de que agora posso dizer ao mundo que comprometi algo valioso com esse problema é validador”.

Sem entrar em detalhes, a prova funciona da seguinte forma: primeiro, Baek disse que o sofá ideal, seja lá do que for, tinha que ter três propriedades específicas: ser monótono, equilibrado e ter um ângulo de rotação π/2 – praticamente o mesmo “sofá” em formato de meia rosquinha que já havia sido imaginado.

Em segundo lugar, Baek começou a provar uma condição sobre como esse sofá se moveria ao redor do canto. Isso pode parecer simples, mas foi crucial para verificar que o limite superior para a área desse sofá era igual ao limite inferior de Gerver.

Na prática, isso significa que Baek provou que Gerver esteve certo todos esses anos. Procurado pela New Scientist, o cientista (que hoje tem 75 anos) afirma que está “muito feliz”: “Estou orgulhoso que Baek tenha pegado o bastão e terminado o que comecei”, conclui.

Antes de colocar o ponto final na questão, a solução proposta ainda deverá ser revisada por pares, que vão assegurar a legitimidade dos cálculos. Mas, ao que tudo indica, o problema do sofá foi, por fim, respondido após 58 anos.